

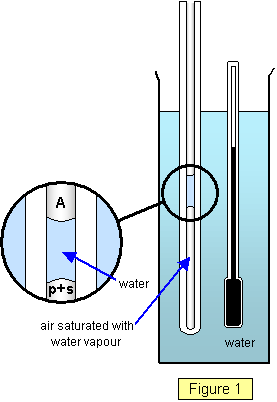
This is a simple method, for which the
apparatus is shown in Figure 1: a capillary tube closed at one end containing a short column
of air with a water plug stands in a glass of water. The air trapped in the tube is of course
saturated since there is excess water present.
Let the atmospheric pressure be A,
let the air pressure in the tube be p and the s.v.p. of water at that temperature be s.
Neglecting the weight of the small amount of water in the plug, we
have
Therefore:
p = A - s
Now saturated vapours do not obey
Boyle's law, because their pressure is constant at a given temperature and is independent of
the volume of air. Therefore for the air in the tube we have:
(A - s)V/T =
constant
where V is the volume of air in the tube and T is its
temperature.
We can therefore measure the s.v.p. of water if its value at one
temperature is known.
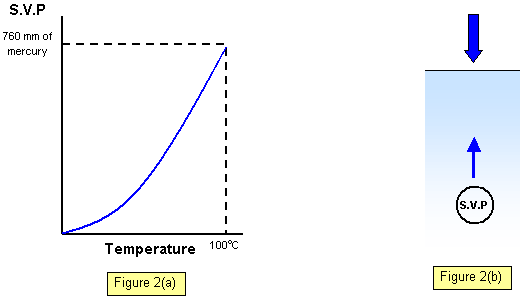
The results obtained for water are
shown in Figure 2(a). Notice that the s.v.p. rises with temperature as predicted, and that its
value at 100 oC is the value of standard atmospheric pressure. This fact can be explained as
follows. Consider a bubble below the surface of the liquid: the pressure within the bubble is
the saturated vapour pressure of that liquid, neglecting the hydrostatic pressure which is
comparatively small.
Now when the liquid boils bubbles rise to the surface of the
liquid and escape so the pressure within them must be equal to the external pressure
(Figure 2(b).
We can say, therefore, that: